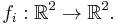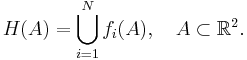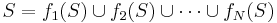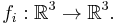Fractal compression
Fractal compression is a lossy compression method for digital images, based on fractals. The method is best suited for textures and natural images, relying on the fact that parts of an image often resemble other parts of the same image. Fractal algorithms convert these parts into mathematical data called "fractal codes" which are used to recreate the encoded image.
Contents |
Iterated Function Systems
Fractal image representation can be described mathematically as an iterated function system (IFS).
For Binary Images
We begin with the representation of a binary image, where the image may be thought of as a subset of 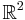 . An IFS is a set of contraction mappings ƒ1,...,ƒN,
. An IFS is a set of contraction mappings ƒ1,...,ƒN,
According to these mapping functions, the IFS describes a two-dimensional set S as the fixed point of the Hutchinson operator
That is, H is an operator mapping sets to sets, and S is the unique set satisfying H(S) = S. The idea is to construct the IFS such that this set S is the input binary image. The set S can be recovered from the IFS by fixed point iteration: for any nonempty compact initial set A0, the iteration Ak+1 = H(Ak) converges to S.
The set S is self-similar because H(S) = S implies that S is a union of mapped copies of itself:
So we see the IFS is a fractal representation of S.
Extension to Grayscale
IFS representation can be extended to a grayscale image by considering the image's graph as a subset of 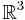 . For a grayscale image u(x,y), consider the set S = {(x,y,u(x,y))}. Then similar to the binary case, S is described by an IFS using a set of contraction mappings ƒ1,...,ƒN, but in
. For a grayscale image u(x,y), consider the set S = {(x,y,u(x,y))}. Then similar to the binary case, S is described by an IFS using a set of contraction mappings ƒ1,...,ƒN, but in 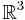 ,
,
Encoding
A challenging problem of ongoing research in fractal image representation is how to choose the ƒ1,...,ƒN such that its fixed point approximates the input image, and how to do this efficiently. A simple approach[1] for doing so is the following:
- Partition the image domain into blocks Ri of size s×s.
- For each Ri, search the image to find a block Di of size 2s×2s that is very similar to Ri.
- Select the mapping functions such that H(Di) = Ri for each i.
In the second step, it is important to find a similar block so that the IFS accurately represents the input image, so a sufficient number of candidate blocks for Di need to be considered. On the other hand, a large search considering many blocks is computationally costly. This bottleneck of searching for similar blocks is why fractal encoding is much slower than for example DCT and wavelet based image representations.
Features
With fractal compression, encoding is extremely computationally expensive because of the search used to find the self-similarities. Decoding, however is quite fast. While this asymmetry has so far made it impractical for real time applications, when video is archived for distribution from disk storage or file downloads fractal compression becomes more competitive.[2][3]
At common compression ratios, up to about 50:1, Fractal compression provides similar results to DCT-based algorithms such as JPEG. [4] At high compression ratios fractal compression may offer superior quality. For satellite imagery, ratios of over 170:1[5] have been achieved with acceptable results. Fractal video compression ratios of 25:1-244:1 have been achieved in reasonable compression times (2.4 to 66 sec/frame).[6]
Compression efficiency increases with higher image complexity and color depth, compared to simple grayscale images.
Resolution independence and fractal scaling
An inherent feature of fractal compression is that images become resolution independent[7] after being converted to fractal code. This is because the iterated function systems in the compressed file scale indefinitely. This indefinite scaling property of a fractal is known as "fractal scaling".
Fractal interpolation
The resolution independence of a fractal-encoded image can be used to increase the display resolution of an image. This process is also known as "fractal interpolation". In fractal interpolation, an image is encoded into fractal codes via fractal compression, and subsequently decompressed at a higher resolution. The result is an up-sampled image in which iterated function systems have been used as the interpolant.[8] Fractal interpolation maintains geometric detail very well compared to traditional interpolation methods like bilinear interpolation and bicubic interpolation.[9][10][11]
History
Michael Barnsley led development of fractal compression in 1987, and was granted several patents on the technology.[12] The most widely known practical fractal compression algorithm was invented by Barnsley and Alan Sloan. Barnsley's graduate student Arnaud Jacquin implemented the first automatic algorithm in software in 1992.[13][14] All methods are based on the fractal transform using iterated function systems. Michael Barnsley and Alan Sloan formed Iterated Systems Inc.[15] in 1987 which was granted over 20 additional patents related to fractal compression.
A major breakthrough for Iterated Systems Inc. was the automatic fractal transform process which eliminated the need for human intervention during compression as was the case in early experimentation with fractal compression technology. In 1992 Iterated Systems Inc. received a $2.1 million government grant[16] to develop a prototype digital image storage and decompression chip using fractal transform image compression technology.
Fractal image compression has been used in a number of commercial applications: onOne Software, developed under license from Iterated Systems Inc., Genuine Fractals 5[17] which is a Photoshop plugin capable of saving files in compressed FIF (Fractal Image Format). To date the most successful use of still fractal image compression is by Microsoft in its Encarta multimedia encyclopedia,[18] also under license.
Iterated Systems Inc. supplied a shareware encoder (Fractal Imager), a stand alone decoder, a Netscape plug-in decoder and a development package for use under Windows. As wavelet-based methods of image compression improved and were more easily licensed by commercial software vendors the adoption of the Fractal Image Format failed to evolve.
During the 1990s Iterated Systems Inc. and its partners expended considerable resources to bring fractal compression to video. While compression results were promising, computer hardware of that time lacked the processing power for fractal video compression to be practical beyond a few select usages. Up to 15 hours were required to compress a single minute of video.
ClearVideo — also known as RealVideo (Fractal) — and SoftVideo were early fractal video compression products. ClearFusion was Iterated's freely distributed streaming video plugin for web browsers. In 1994 SoftVideo was licensed to Spectrum Holobyte for use in its CD-ROM games including Falcon Gold and Star Trek: The Next Generation A Final Unity.[19]
In 1996 Iterated Systems Inc. announced[20] an alliance with the Mitsubishi Corporation to market ClearVideo to their Japanese customers. The original ClearVideo 1.2 decoder driver is still supported[21] by Microsoft in Windows Media Player although the encoder is no longer supported.
Numerous research papers have been published during the past few years discussing possible solutions to improve fractal algorithms and encoding hardware.[22][23][24][25][26][27][28][29][30]
Open Source
A library called Fiasco was created by Ullrich Hafner and described in Linux Journal.[31]
The Netpbm library includes a Fiasco library. [32] [33]
There is a video library for fractal compression. [34]
There is another example implementation from Femtosoft. [35]
See also
Notes
- ^ Fischer, Y. (1992). "Fractal Image Compression". SIGGRAPH'92 course notes.
- ^ Image Compression Alternatives and Media Storage Considerations Georgia Institute of Technology reference to compression/decompression time.
- ^ Heath, Steve (1999). Multimedia and Communications Technology. Focal Press. pp. 120–123. ISBN 0240515293.
- ^ Sayood, Khalid (2005). Introduction to Data Compression, Third Edition. Morgan Kaufmann. pp. 560–569. ISBN 012620862X.
- ^ Geoscience and Remote Sensing Symposium paper Achieving high data compression of self-similar satellite images using fractal.
- ^ Fractal encoding of video sequences
- ^ Walking, Talking Web Byte Magazine article on fractal compression/resolution independence
- ^ Interpolation decoding method with variable parameters for fractal image compression College of Mathematics and Physics, Chongqing University, China
- ^ Smooth fractal interpolation Departamento de Matemáticas, Universidad de Zaragoza, Campus Plaza de San Francisco, Zaragoza, Spain
- ^ A Note on Expantion Technique for Self-Affine Fractal Objects Using Extended Fractal Interpolation Functions Hokkaido Univ., Graduate School of Engineering, JPN
- ^ Studies on Scaling Factor for Fractal Image Coding Nagasaki University, Faculty of Engineering
- ^ U.S. Patent 4,941,193 – Barnsley and Sloan's first iterated function system patent, filed in October 1987
- ^ Using Fractal Coding to Index Image Content for a Digital Library Tech report
- ^ Arnaud E. Jacquin. Image Coding Based on a Fractal Theory of Iterated Contractive Image Transformations. IEEE Transactions on Image Processing, 1(1), 1992.
- ^ Iterated Systems Inc. changed its name to MediaBin Inc. Inc. in 2001 and in turn was bought out by Interwoven, Inc. in 2003)
- ^ government grant
- ^ Genuine Fractals Product Review
- ^ Mathematics Awareness Week - April 1998 reference to Microsoft's Encarta fractal image compression
- ^ 1994 Manual specifying on page 11 SoftVideo under license to Spectrum Holobyte
- ^ Mitsubishi Corporation ClearVideo press release
- ^ Microsoft ClearVideo support
- ^ Advances in fractal compression for multimedia applications
- ^ Fast calculation of IFS parameters for fractal image coding
- ^ Fractal image compression performance synthesis through HV partitioning
- ^ Simple and Fast Fractal Image Compression Circuits, Signals, and Systems - 2003
- ^ Schema genetic algorithm for fractal image compression Department of Electrical Engineering, National Sun Yet-Sen University, Kaohsiung, Taiwan
- ^ A fast fractal image encoding method based on intelligent search of standard deviation Department of Electrical and Computer Engineering, The University of Alabama
- ^ Novel fractal image-encoding algorithm based on a full-binary-tree searchless iterated function system Department of Electrical and Computer Engineering, The University of Alabama
- ^ Fast classification method for fractal image compression Proc. SPIE Vol. 4122, p. 190-193, Mathematics and Applications of Data/Image Coding, Compression, and Encryption III, Mark S. Schmalz; Ed
- ^ Toward Real Time Fractal Image Compression Using Graphics Hardware Dipartimento di Informatica e Applicazioni, Università degli Studi di Salerno
- ^ http://www.linuxjournal.com/article/4367
- ^ http://netpbm.sourceforge.net/doc/pnmtofiasco.html
- ^ http://netpbm.sourceforge.net/doc/fiascotopnm.html
- ^ http://castor.am.gdynia.pl/cgi-bin/man/man2html?3+fiasco_decoder_get_frame
- ^ http://www.femtosoft.biz/fractals/fractal.html
External links
- Pulcini and Verrando's Compressor
- Waterloo Fractal Coding Project Formerly the Waterloo Fractal Compression Project
- Keith Howell's 1993 M.Sc. dissertation Fractal Image Compression for Spaceborne Transputers
- My Main Squeeze: Fractal Compression, Nov 1993, Wired.
- Fractal Basics description at FileFormat.Info
- Superfractals website devoted to fractals by the inventor of fractal compression
|
||||||||||||||||||||||||||||||||||||||||||||||||||||